Our towns, villages and regions
Oziemb這wski surname in Poland in year 2002
Classical
genealogy
(PDF'S in English and Polish)
Another
graphics
(coat of arms)


I1-M253P (I1-ASP) subclade
using of "multidimensional scaling" and "cluster analysis"
author: Maciej Oziemb這wski
Two
identical (for Y67) haplotypes of two men with Oziemb這wski surname
(kit 169071 and 191847) are part of ASP subclad
(Anglosaxon in Polish/Pomeranian/Prussian variant). These haplotypes
are treated as 1 common haplotype "Oziemblowski" in the next
part of the text. More about I1-ASP subclad you can find in Polish language
on my another web site in the context of FT-DNA
project "Normans-CE".
I wanted to check the standard statistical analysis (with use of Statistica
9.0 software) like "multidimensional scaling" [MS] and "cluster
analysis" [CA] for clustering of haplotypes within the I1-M253P
(I1-ASP) subclad (according to data on 10 Oct., 2010).
1) 20 haplotypes of STR 67 markers Y-DNA were taken from Normans-CE project and 2 haplotypes from Ysearch database (i.e. Matz, Reck) classified into I1-ASP subclade by Peter Gwozdz, so there were 22 haplotypes taken for study. Values of 67 STR Y-DNA markers for all 22 haplotypes can be found in Tab. 1 (three parts: 1a, 1b, 1c).
2) The next step was the standardization of data. The reason for that procedure was to avoid effect that the markers with value of eg 34-35 would be "stronger" in the model as compared to markers with eg 8-9 value. New values after standardization can be found in Tab. 2a and 2b. Identical marker values within all 22 haplotypes occured for 22 markers, so there were finally only 45 markers (67-22=45) taken into account for the next step.
3) "Distance matrix" was created according to Tab. 2, what was shown in Tab. 3. There is "a number" for each pair of compared haplotypes. Higher numbers = less similarity between compared pairs of haplotypes. Smaller numbers = more similarity between compared pairs of haplotypes.
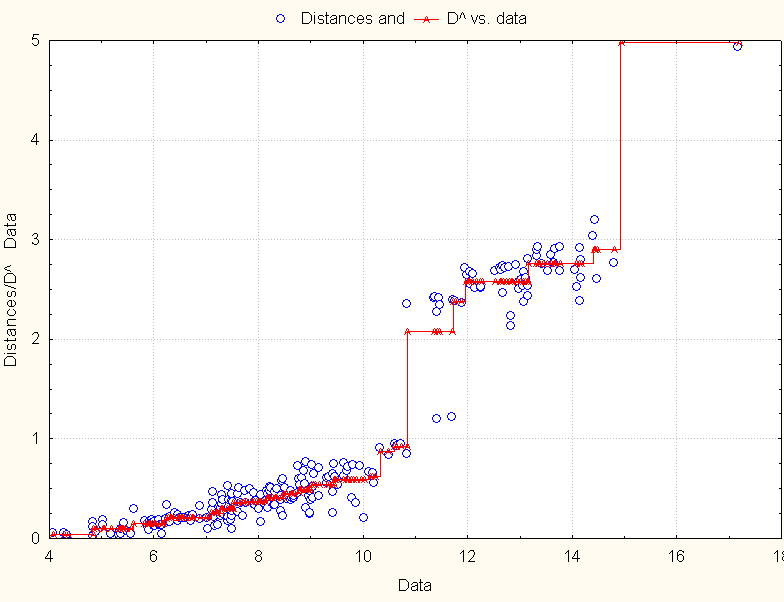
4) Matrix in the Tab. 3 was the base for the next calculations in the multidimensional scaling method. It was stated (according to Fig. 1) that 2 or 3-dimensional model will be good for the next calculations. 2-D model was finally chosen. Shepard's Diagram (Fig. 2) confirmed, that 2-D model correct described similarity of STR Y-DNA haplotype pairs (points are close to "stairs"). Each point on Fig. 3 represents one pair of compared haplotypes. Some points are overlapped, but there is 231 pairs of compared haplotypes what can be calculated with the use of Newton binomial or direct from the next expression: (22*21)/2.
Fig.
1
"Scree" diagram for 22 haplotypes=persons
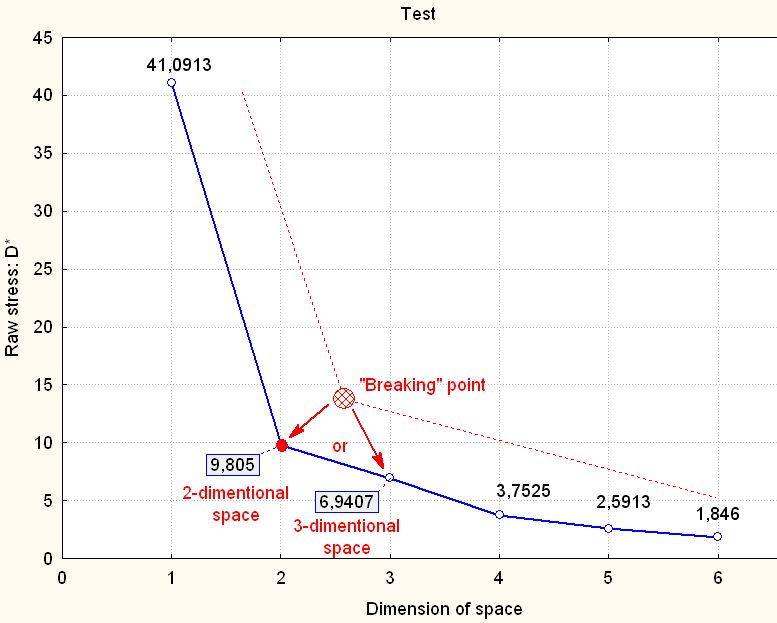
Fig.
2
Shepard's diagram for 22 haplotypes=persons
5) Similarity of 22 haplotypes (persons) is shown on the 2-dimentional model (i.e. on surface). Points closer to each other = higher similarity of haplotypes. Three haplotypes are the most different as compared to the next 19 haplotypes. That 3 haplotypes are in "Far outher space".
Fig.
3
Similarity of 22 haplotypes in 2-D model

6) Two groups of haplotypes can be manually "demacrated" when "zooming-in" into 19 haplotypes (Fig. 4): "Middle Outer Space" and "Inner Space". These 19 points are a little moved right (as compared to 0,0 point) because of the most different 3 points (Fig. 3) influence. Fig. 4 shows 19 points on selected surface of 22 haplotypes 2-D model.
Fig.
4
Similarity of 22 haplotypes in 2-D model
(but there is "zoom-in" showing only 19 haplotypes)

7) Three the most different haplotypes were excluded from the next model. The same steps for 19 haplotypes were repeated: "scree" diagram and choosing of 2-D model (Fig. 5) and later Shepard's diagram (Fig. 6) which seems to be OK (points representing all of haplotypes pairs are close to "stairs"). There were only 171 pairs of haplotypes to be compared [171 = (19*18)/2]. 2-D model was plotted for 19 haplotypes (Fig. 7). It was found 10 haplotypes located in nucleus cluster in the centre of coordinate system ("Inner space"). Bembnista and Pietruszewski haplotypes were the most close to 0,0 point. Johnsen haplotype (one of the 9 haplotypes from "Middle outer space") was the most close to "Inner space" haplotypes. Each new haplotype added to (or removed from) model has influence on points (or haplotypes=persons) distribution onto multidimenstional model (for instance 2-D model = surface). Each new haplotype "brings" something new into model and each removed haplotype "takes something away" from the model.
Fig.
5
"Scree" diagram for 19 haplotypes=persons
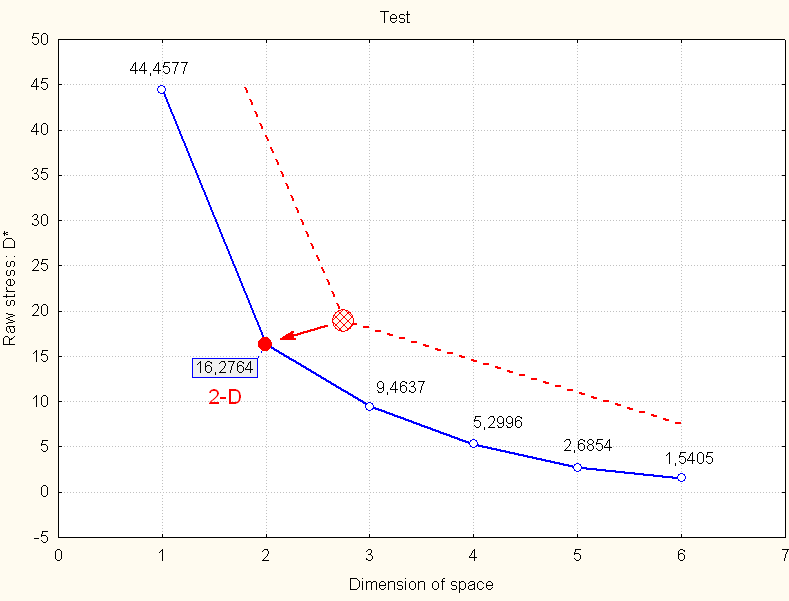
Fig.
6
Shepard's diagram for 19 haplotypes=persons
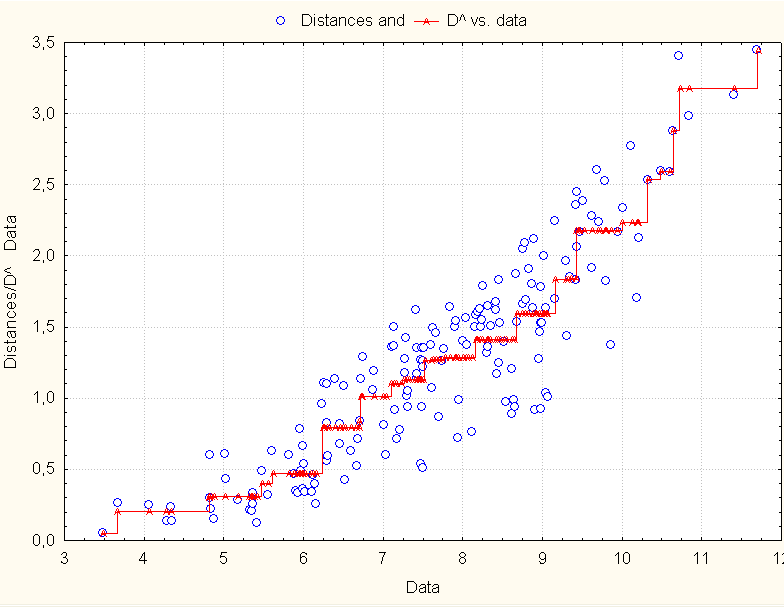
Fig.
7
Similarity of 19 haplotypes in 2-D model

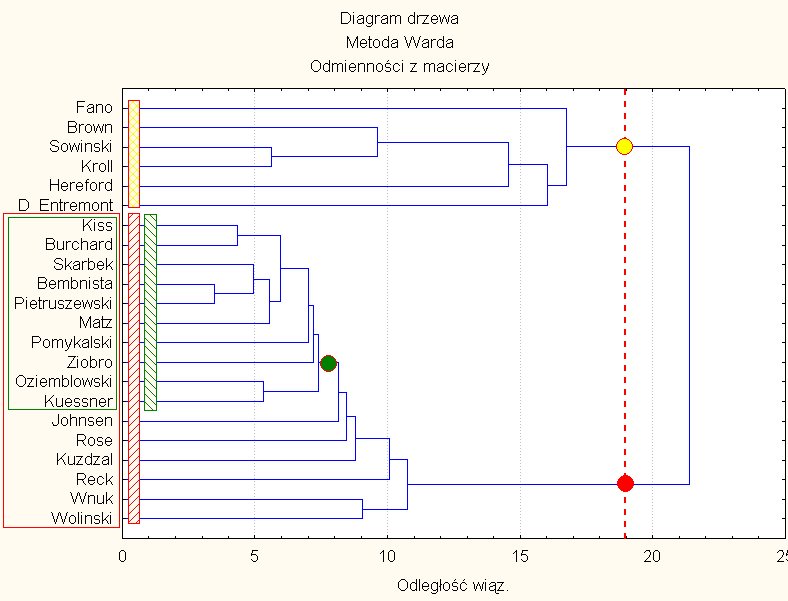
9) There were 5 tree diagrams plotted (Fig. 8-12) as a results of 5 different ways of "binder", i.e.: single binder method (Fig. 8), full binder method (Fig. 9), average binder (Fig. 10), specific gravity method (Fig. 11) and Ward's methods (Fig. 12). Fig. 8-12 confirmed generally observations from "Multidimensional scaling" method, but the matrix used in both methods (MS & CA) was the same. Nevertheless a little another clusters were created in Ward's methods of "Cluster analysis".
Fig.
8
Similarity of 22 haplotypes in "single binder method"

Fig.
9
Similarity of 22 haplotypes in "full binder method"
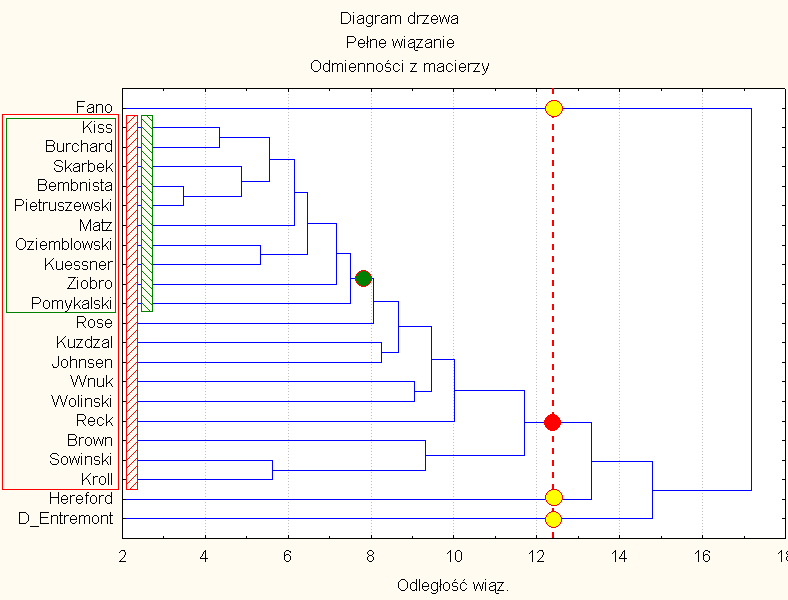
Fig.
10
Similarity of 22 haplotypes in "average binder method"

Fig.
11
Similarity of 22 haplotypes in "specific gravity method"
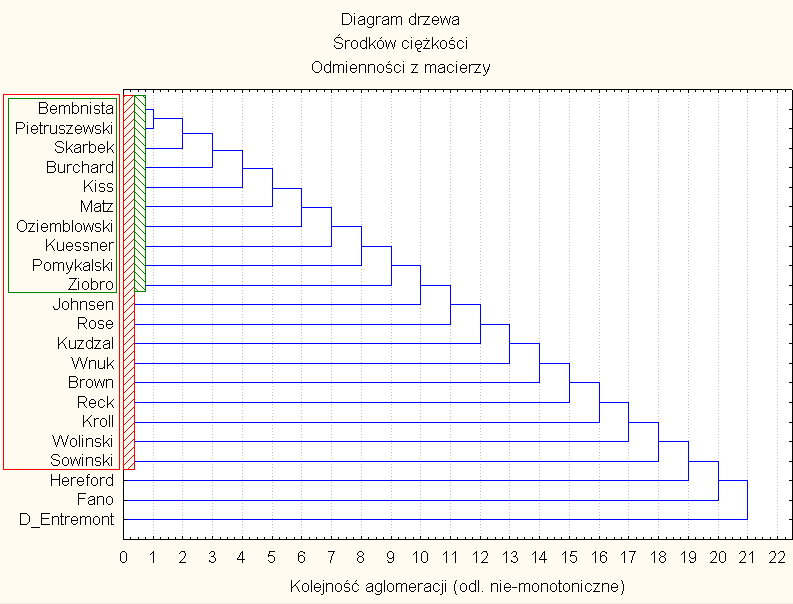
Fig.
12
Similarity of 22 haplotypes in "Ward's method"